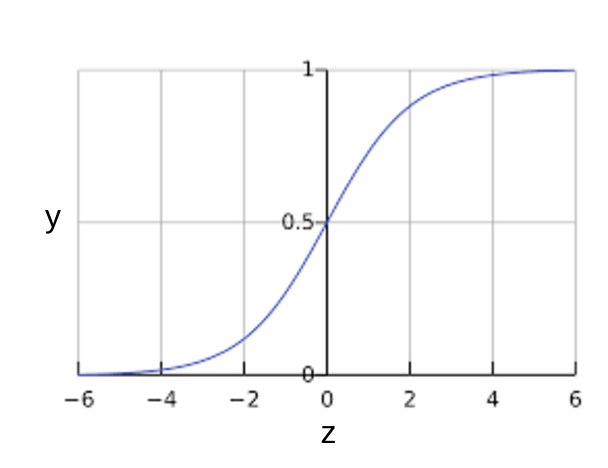
Sigmoid Function

0, if $\sum w_i x_i \le 0$. For example: $\sigma(-10) = 0$
1, if $\sum w_i x_i \gt 0$. For example: $\sigma(10) = 1$
$$\sigma(z) = \frac{1}{1+e^{-z}} $$

---

Loss Function

L(a,b) find a, b. And minimise the loss function.

$$ L(a,b) = -y_i log h_i - (1-y_i) log(h-h_i) $$

If $y_i = 0$, then $L = -1-log(1-h_i) $
If $y_i = 1$, then $L = -log h_i $

---

One dimensional Case

Passing the linear regression with sigma $(\sigma)$ function will be logistic regression.
$$ h = \sigma (ax+b) $$

a = $ a - \frac{\partial L}{\partial a} * \alpha $

b = $ b - \frac{\partial L}{\partial b} * \alpha $

$$ \frac{\partial L}{\partial a} = \frac{1}{N} \sum_{i=1}^N (h_i - y_i) * x_i $$

$$ \frac{\partial L}{\partial b} = \frac{1}{N} \sum_{i=1}^N (h_i - y_i) $$

---

Multi-Dimensional Case

$$ h = \sigma (\sum_{i=1}^N (w_i * x_i) + b) $$

---

Normal Distribution

Logistic will not need apply normal distribution for out range value.

For more info about using Normal Distribution.

---

Batch

The way of Logistic Regression using Batch is same way as Linear Regression to use Batch.

For more info about using Batch

---

Sigmoid Derivative

$$ \frac{d}{dx}\sigma(x) = \sigma(x) * (1 - \sigma(x)) $$

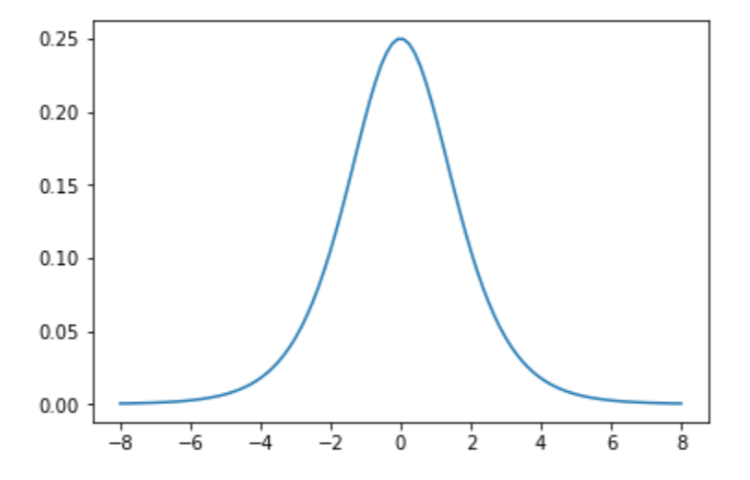
def sigmoid_derivative(x):
    return sigmoid(x) * (1 - sigmoid(x))

---

Precision & Recall

Precision = True positive / No. of predicted positive
Recall = True positive / No. of actual positive
F1_score = $2\frac{PR}{P+R}$

---

2019-04-29